Searching and Sorting Explanation

Sequential Search

Sequential search simply traverses the array, looking at each value until it finds a match. It has a worst case time complexity of O(n).

							
public int seqSearch(int [] arr, int val){
	for (int i = 0; i < arr.length; i++){
		if (val == arr[i]){
			return i;
		}
	}
	return -1;
}

Binary Search

Binary search uses the programming paradigm of Divide and Conquer to split the problem up into continuously smaller pieces. It does this by splitting the array in half. It takes the middle value of the sorted array as a divider. If the value we are looking for is less than the middle, then it must be in the first half. If the value we are looking for is greater than the middle, then it must be in the second half. If the value we are looking for is equal to the middle, then we have found the location of the value. We then repeat this process, running binary search on the half where the value is. When the half that we are looking at has a size of less than 1, we can assume that the value is not found in the array. Although this algorithm may seem like a good candidate for recursion, it is generally programmed in an iterative manner to ensure that it is fast. This will run with a time complexity of O(log n).

							
public int binarySearch(int [] arr, int val){
	int left = 0;
	int right = arr.length-1;
	while (right-left > 0){
		int middle = (left+right)/2;
		int middleVal = arr[middle];
		if (val > middleVal){
			left = middleVal+1;
		}
		else if (val < middleVal){
right = middleVal-1;
		}
		else{
			return middle;
		}
	}
	return -1;
}

A sorting algorithm organizes an array into ascending or descending order.
Quicksort is a divide and conquer sorting algorithm that is considered to be one of the quickest sorts available. It is used in many different applications, and is an industry standard among programming languages like Java, C, and many more.

How it Works

Quicksort will work via these fundamental steps:

1. Find a pivot for the array
2. Split the array so that the values smaller than the pivot are on the left side, and the values larger than the pivot are on the right side.
3. Repeat steps 1 and 2 for the smaller side and larger side.
4. Base case is when the subarray section has a size less than one (left pointer is greater than right pointer)

Let’s begin with the first step. There are many ways to select a pivot. In most situations, the pivot is either selected as the right most indexed value or the median value between the left most indexed value, the middle value, and the right most indexed value. This is to attempt to avoid bad pivot selection. We will be sticking with right most indexed value for simplicity’s sake.

For the next step, there are two algorithms: Lomuto and Hoare. Lomuto is less optimal than Hoare but is easier to understand.

Have a pointer which begins at the first element of the array or subarray. Traverse the array fully except the last element, as that will be the pivot. Check if the value you are currently on is less than the pivot. If it is, swap it with the element at the pointer. Move the pointer forward, as the value you have just swapped in will be in the correct position and should not be swapped again. After the traversal, simply swap the pivot with the pointer position and the pivot will be in the right place.

							
public static int findPivot(int [] a, int left, int right){ //left right to make it easier to define subarrays
        int pivot = a[right];
        int index = left;
        for (int i = left; i < right; i++){
            if (a[i] < pivot){
                swap(a, index, i); //helper method that swaps two values in an array.
                index++;
            }
        }
        swap(a, index, right);
        return index;
    }

Here’s an animation of the Lomuto algorithm running on an array.

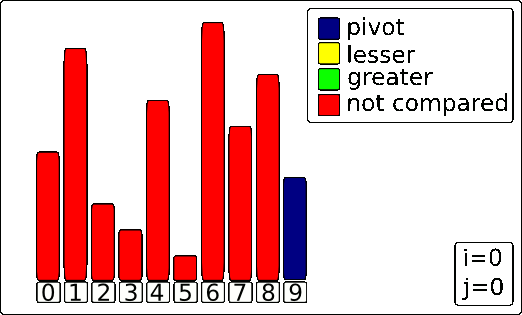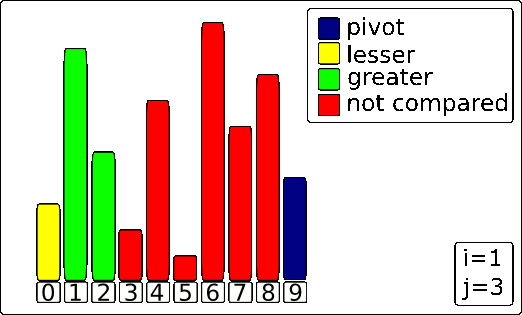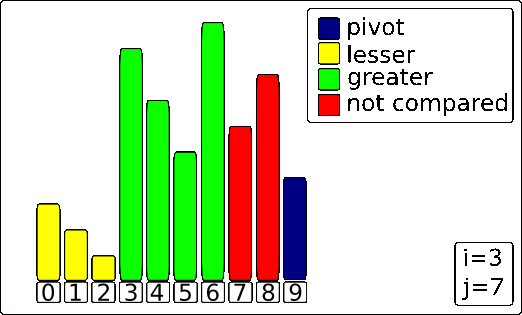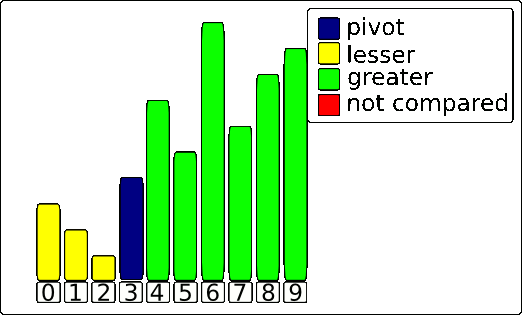
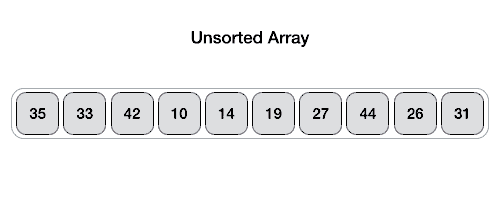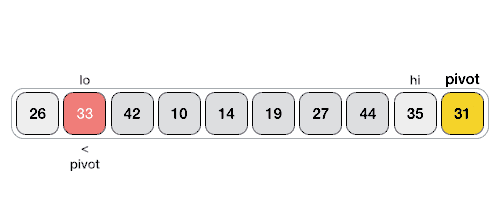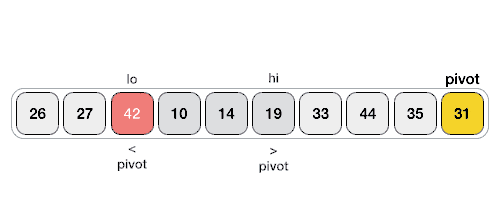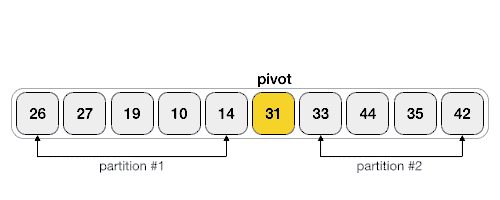
Have two pointers, one beginning at the first element of the array or subarray, and the other beginning at one element before the last element. Check if the left pointer element is smaller than the pivot. If it is, then it is in the correct position. The left pointer then increments. This continues until the left pointer is larger than the pivot. Next, check if the right pointer element is greater than the pivot. If so, decrement the right pointer element until it is less than the pivot. Therefore, after these steps, we will have an inversion, where the left pointer element is in the wrong place and the right pointer element is also in the wrong place. We first check if the left pointer is larger than the right pointer. If so, we have reached the end of the algorithm. Simply swap the pivot with the left element. Otherwise, we swap the two elements since that would put both elements in the correct position. Repeat this process until it terminates because the left pointer is larger than the right pointer.

							
public static int findPivot(int [] a, int left, int right){
        int pivot = a[right];
        if (right == 0){
            return right;
        }
        right--;
        int leftIndex = left;
        int rightIndex = right;
        System.out.println("The pivot is: " + pivot + " for the array " + subArray(a, left, right));
        while(true){
            int leftValue = a[left];
            int rightValue = a[right];
            while(leftValue < pivot){
                left++;
                leftValue = a[left];
            }
            while(right > 0 && rightValue > pivot){
                right--;
                rightValue = a[right];
            }
            if (left >= right){
                System.out.println(Arrays.toString(a)+ " before swap " + left + " " + right);
                swap(a, left, rightIndex+1);
                System.out.println(Arrays.toString(a) + " after swap");
                return left;
            }
            else{
                System.out.println(Arrays.toString(a)+ " before swap " + left + " " + right);
                swap(a, left, right);
                System.out.println(Arrays.toString(a) + " after swap " + right + " " + left);
                left++;
                right--;
            }
        }
}
	

Here’s an animation showing the Hoare algorithm in action.